算法知识

无标签

算法

发布日期: 2022-01-26

文章字数: 332

阅读次数:

判断链表是否有环

使用快慢指针，当他们相遇时，则有环

bool IsExitsLoop(slist *head)
{
    slist *slow = head, *fast = head;

    while ( fast && fast->next ) 
    {
        slow = slow->next;
        fast = fast->next->next;
        if ( slow == fast ) break;
    }

    return !(fast == NULL || fast->next == NULL);
}

找到环的入口

参考博客地址：http://www.cppblog.com/humanchao/archive/2012/11/12/47357.html

公式推导：

快指针经过的路径：2s

慢指针经过的路径：s

nr：走了n圈

假设真个链表长度为L，入环口与相遇点距离为x，起点到入环口的距离为a

则有：

2s = s + nr
s = nr


a + x = nr
a + x = (n - 1)r + r = (n-1)r + L - a
a = (n - 1)r + (L - a - x)

由公式推导可知，只需要我们让两个指针分别指向起点和相遇的点，每次分别next走一步，则一定会在入环点相遇。

求环的大小

只需让这两个快慢指针，继续在环里面走，再次相遇时，所走的步数 = 环的长度

背包问题

01背包求最大值

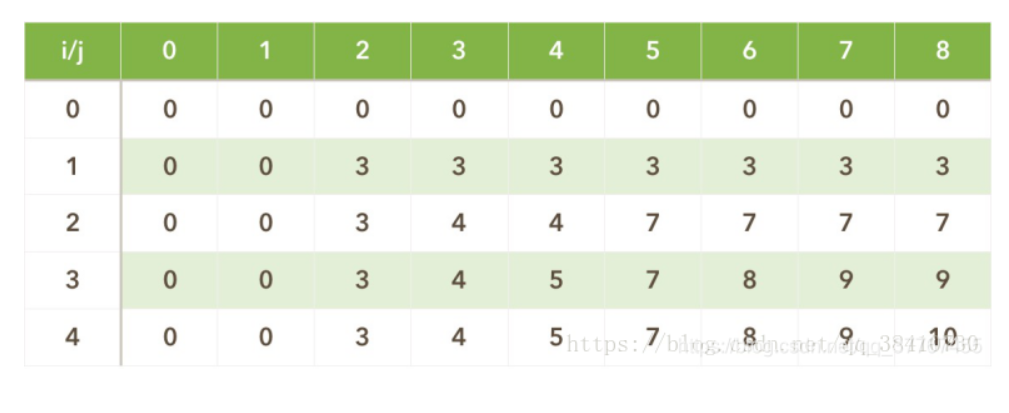
x轴代表bag的容量提升，y轴代表不同物体的序号

物品定义：

int w[5] = { 0 , 2 , 3 , 4 , 5 };            //商品的体积2、3、4、5
int v[5] = { 0 , 3 , 4 , 5 , 6 };            //商品的价值3、4、5、6
int bagV = 8;                            //背包大小

状态转移方程：

for (int i = 1; i <= 4; i++) {
        for (int j = 1; j <= bagV; j++) {
            if (j < w[i])
                dp[i][j] = dp[i - 1][j];
            else
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i]);
        }
    }

完全背包问题求最大值

而完全背包问题只需在01背包上做延伸就可以了，即原来的状态转移方程式改为：

if (j < w[i])
    dp[i][j] = dp[i - 1][j];
else
    dp[i][j] = max(dp[i - 1][j], dp[i][j - w[i]] + v[i]);

用i的原因

因为完全背包，即物品可以重复叠加，即我们应该从本行中提取，不断更新本行的数据

背包问题之装满背包的方案总数

(详情可以查看以下博主的讲解 https://blog.csdn.net/wumuzi520/article/details/7021210)

对于01背包，设置初始值

F[0][0] = 1
F[1~n][0] = 1
F[0][1~m] = 0

状态转移方程式

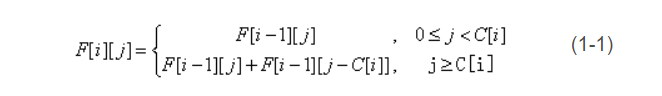
然后就可以计算填满当前（每一列 j 都是对应不同的背包容量时的数量）背包容量时的总数

而完全背包的状态转移方程是则应该为

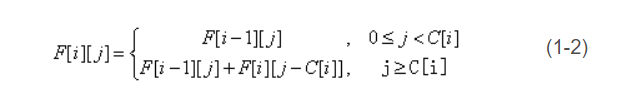
原理和原来求最大值是一样的

在leetcode上总结的背包问题分类：

组合问题：

dp[i] += dp[i-num]

True、False问题

dp[i] = dp[i] or dp[i-num]

最大最小问题

dp[i] = min(dp[i], dp[i-num]+1)或者dp[i] = max(dp[i], dp[i-num]+1)

然后再考虑是01 or 完全背包，是否要考虑顺序

假设target为范围、容量大小，数组nums为物品，则有

如果求组合数就是nums放在外循环，target在内循环
如果求排列数就是外层for遍历背包，内层for循环遍历物品。

异或

异或的性质

两个数字异或的结果a^b是将 a 和 b 的二进制每一位进行运算，得出的数字。运算的逻辑是
如果同一位的数字相同则为 0，不同则为 1

异或的规律

任何数和本身异或则为 0
任何数和 0 异或是本身
异或满足交换律。即 a ^ b ^ c ，等价于 a ^ c ^ b

所以它可用于直接解决：一个数字出现一次，其他都出现了两次，让我们找到出现一次的数的问题

时间复杂度：O(N)，其中N为数组长度。
空间复杂度：O(1)

LRU算法

LRU是Least Recently Used的缩写，也被称为最近最少使用算法，淘汰掉最近很少被使用的数据

/**
 * @param {number} capacity
 */
var LRUCache = function(capacity) {
    this.limit = capacity
    this.arr = []
    this.map = new Map()
};

/** 
 * @param {number} key
 * @return {number}
 */
LRUCache.prototype.get = function(key) {
    if(!this.map.has(key))return -1
    const index = this.arr.indexOf(key)
    for(let i = index; i > 0; i--) {
        this.arr[i] = this.arr[i-1]
    }
    this.arr[0] = key
    return this.map.get(key)
};

/** 
 * @param {number} key 
 * @param {number} value
 * @return {void}
 */
LRUCache.prototype.put = function(key, value) {
    this.map.set(key, value)
    const index = this.arr.indexOf(key)
    if(index !== -1){
        this.arr.splice(index, 1)
    }
    this.arr.unshift(key)
    if(this.arr.length > this.limit){
        const pop = this.arr.pop()
        this.map.delete(pop)
    }
};

/**
 * Your LRUCache object will be instantiated and called as such:
 * var obj = new LRUCache(capacity)
 * var param_1 = obj.get(key)
 * obj.put(key,value)
 */

如果是利用迭代器的特性，还可以这样用

LRUCache.prototype.get = function (key) {
    const cache = this.cache
    if (cache.has(key)) {
        const value = cache.get(key)
        cache.delete(key)
        cache.set(key, value)
        return value
    } else {
        return -1
    }
};
LRUCache.prototype.put = function (key, value) {
    const cache = this.cache
    if (cache.has(key)) cache.delete(key)
    if (cache.size === this.max) cache.delete(cache.keys().next().value)
    cache.set(key, value)
};

LFU算法

Least Frequently Used

也被称为最近最少访问频率，他有两个维度，一个是访问频率，一个是时间最近

实质上就是添加多个一哈希表用于记录访问频率

var LFUCache = function(capacity) {
  this.size = capacity
  this.valueMap = new Map()     // 记录值
  this.useMap = new Map()       // 记录使用次数
};

LFUCache.prototype.get = function(key) {
  if (this.valueMap.has(key)){       // 当存在时 删掉原来的重新添加  使用值加1
    let use = this.useMap.get(key)
    let value = this.valueMap.get(key)
    this.valueMap.delete(key)
    this.useMap.set(key, use + 1)
    this.valueMap.set(key, value)
    return value
  } else {
    return -1
  }
};

LFUCache.prototype.put = function(key, value) {
  if(this.size === 0) return
  let min = Math.min(...this.useMap.values())  // 缓存下 最小使用值
  if (this.valueMap.has(key)) {                // 如果存在 值重新赋, use加一
    this.valueMap.set(key, value)
    let use = this.useMap.get(key)
    this.useMap.set(key, use + 1)
  } else {                                     // 不存在就直接加
    this.valueMap.set(key, value)
    this.useMap.set(key, 1)
  }
  // 当超出, 删掉不常用的 当碰到用的次数相同的删掉 较前未使用的
  if(this.valueMap.size > this.size){
    let it = this.valueMap.keys()              // 缓存 key 遍历器
    let delKey = it.next().value
    while(this.useMap.get(delKey) !== min){    // 获取使用值为 min 的key
      delKey = it.next().value
    }
    this.useMap.delete(delKey)                 // 删掉该项
    this.valueMap.delete(delKey)
  }
};